Chapter 03 회귀 알고리즘과 모델 규제
앞서 머신러닝의 에는 지도학습과 비지도 학습이 있고 지도학습의 알고리즘에는 분류와 회귀가 있다,
2일 차에 학습한 것은 데이터의 분류에 의해 데이터를 학습하여 결과를 추측하는 형태였다면
회귀는 기존의 데이터의 규칙을 파악하여 임의의 결괏값을 예측하는 것이라고 볼 수 있다.
3-1K 최근접 이웃 회귀
KNN(K-Nearest Neighbors regression)을 이용하면 분류뿐 아니라 회귀 또한 가능하다.
이는 주변값의 평균을 이용하여 회귀를 한다.
오늘은 농어의 데이터 값을 바탕으로 농어의 무게를 추측하는 프로그램을 만들어 보자
import numpy as np
# 농어 데이터 : 회귀 이용
perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0,
21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7,
23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5,
27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0,
39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5,
44.0])
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,
115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,
150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,
218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,
556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,
850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,
1000.0])
#훈련세트와 테스트 세트
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(perch_length,perch_weight, random_state=42)
#2차원 배열로 reshape() 메소드 사용 :
#reshape(-1,1) 로 사용하면 -1은 나머지 원소 개수로 모두 채우라 는 의미이다
train_input = train_input.reshape(-1,1)
test_input = test_input.reshape(-1,1)
print(train_input.shape, test_input.shape)2일 차에 했던 내용과 크게 다르지 않지만 1차원 배열을 2차원으로 만들 때 reshape()를 사용한다는 점이 다르다
reshape(-1,1)이라는 것은 열의 개수를 기준으로 행을 자동으로 배치하게 된다.
(42, 1) (14, 1)
결과를 보면 42행 1열 과 14행 1열의 2차원 데이터가 생겼다는 것을 알 수 있고 배열전체의 개수를 새지 않고 원하는 형태의 구조를 만들 수 있다.
사이킷런에서 k-최근접 이웃 회귀 알고리즘을 구현한 클래스는 KNeighborsRegressor이다.
이는 KNeighborsClassifier과 매우 비슷해서 똑같이 객체를 생성하고 fit, score, predit을 사용한다.
#결정계수 R^2
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor()
#훈련
knr.fit(train_input,train_target)
print(knr.score(test_input, test_target))
0.992809406101064결과를 보면 상당히 높은 점수를 볼 수 있는데 이는 분류에서 평가하는 기준이고 회귀에서는 결정계수를 통해 평가를 한다.
결정계수를 구하는 식은 다음과 같다

이런 결정계수를 구하는 식은 sklearn.metrics 패키지에 포함된 mean_absolute_error를 이용하면 된다.
from sklearn.metrics import mean_absolute_error
test_prediction = knr.predict(test_input)
mae = mean_absolute_error(test_target, test_prediction)
print("평균오차 :",mae)
#테스트세트 사용 평가
print(knr.score(test_input, test_target))
#훈련세트 사용 평가
print(knr.score(train_input, train_target))평균오차 19.157142857142862
0.992809406101064
0.9698823289099254결과를 보면 각 각 테스트 서트의 평가와 훈련세트의 평가를 확인해 보는데 테스트 세트를 사용했때의 결과가 훈련세트를 사용한 것보다 점수가 높은 것을 볼 수 있다. 이러한 경우를 과소 적합이라 추가적으로 둘의 점수가 낮은 경우에도 과소 적합이라고 한다. 이와 반대로 훈련세트가 테스트 세트에 비해 높은 경우는 과대 적합이라고 한다.
두 가지 모두 좋은 결과라고 볼 수 없는데 과소 적합의 경우 모델이 단순할 경우 발생하므로 이를 해결하기 위해 K-최근접 모델의 경우 이웃의 수를 줄여주면 된다. 기본적으로 5개가 이웃으로 설정되어 있으므로 객체의 이웃을 n_neighbors를 이용해서 줄여줄 수 있다.
#K-최근접 이웃 수는 기본적으로 5이고 이를 3으로 줄여보자
knr.n_neighbors = 3 #이웃수 조절
knr.fit(train_input, train_target)
print(knr.score(train_input, train_target))
print(knr.score(test_input, test_target))0.9804899950518966
0.9746459963987609이제 훈련세트가 테스트 세트보다 높고 둘 다 점수가 좋은 결과를 얻을 수 있다.
3-2 선형 회귀
앞선 프로그램에 기존 데이터에 크게 벗어난 정보가 들어가면 어떻게 될까
#만약 데이터값에서 크게 벗어난 정보다 입력된다면 어떻게 될까
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor(n_neighbors= 3)
knr.fit(train_input, train_target)
print(knr.predict([[50]]))다음의 결과는 [1033.33333333]가 나온다. 분명 50이라는 값이 들어가면 적어도 1200 이상의 값이 나와야 하는데 이상하다. 이를 그래프로 확인해 보면
mport matplotlib.pyplot as plt
distances, indexes = knr.kneighbors([[50]])
plt.scatter(train_input, train_target)
plt.scatter(train_input[indexes], train_target[indexes], marker='D')
plt.scatter(50, 1033, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
이를 통해 K- 최근접 모델의 한계를 알 수 있는데, K- 최근접 모델은 인접한 값의 평균치를 계산하여 결과를 찾아내기 때문에 기존값에서 벗어난 정보를 입력하면 오류가 발생하게 된다. 이를 해결하기 위한 방법이 선형 회귀이다.
단순히 정해진범위 내의 값을 예측하는 것은 K-최근접이 좋을 수 있다. 그러나 범위 내에 값을 예측하는 데는 접합하지 않다. 이를 통해 머신러닝을 사용할 때는 상황에 맞는 적절한 모델을 사용하는 것이 중요하다.
선형회귀는 sklearn.linear_model패키지에 있는 LinearRegression 클래스로 선형 회귀 알고리즘을 구현할 수 있다. 선형 회귀 또한 fit, score, predit을 사용한다.
from sklearn.linear_model import LinearRegression
#선형 회귀 모델 생성
lr = LinearRegression()
#선형 회귀 모델 훈련
lr.fit(train_input, train_target)
#선형 회귀 모델 예측
print(lr.predict([[50]]))결과는 [1241.83860323]로 어느 정도 납득할 만한 수치이다. 그러나 이 선형 회귀 모델에는 단점이 있는데
선형 말 그대로 직선의 형태를 띠고 있는데 수식으로 본다면 다음과 같다
농어 무게 = a X 농어의 길이 + b수학시간에 배운 간단한 직선의 방정식으로 a = 기울기 b는 절편이다. LinearRegression 클래스에서는 이 기울기와 절편을 coef_ 와 interecpt_ 를 통해서 구할 수 있다.
print(lr.coef_, lr.intercept_)
=>[39.01714496] -709.0186449535477위 값을 보면 15 이전에는 음수값을 가진다는 것을 볼 수 있는데. 생각보다는 좋은 알고리즘은 아니라는 걸 알 수 있다.
이와 같은 오류를 어떻게 해결할 수 있을까. 방법은 간단한데 수학에서도 직선의 방정식을 배운 다음에
곡선 즉 다항식을 배우게 되는데 회귀 모델도 다항 회귀 모델을 사용하면 해결할 수 있다.
다항 모델을 만드는 방법은 어렵지 않은데 x값인 논의의 길이를 제곱한 값을 항을 훈련세트에 추가하면 된다.
#다항 회귀 :y = a X x^2 + b X x + c
train_poly = np.column_stack((train_input **2,train_input))
test_poly = np.column_stack((test_input **2, test_input))만들어진 데이터셋의 크기를 확인해 보자
print(train_poly.shape, test_poly.shape)
=> (42, 2) (14, 2)
원하는 데로 크기가 늘어난 것을 알 수 있다. 이제 train_poly를 추가해 학습하고 결과를 알아보자
여기서 주의할 점이 있는데 predict을 할 때 다항 회귀의 경우 입력값이 2개인 것을 유의해야 한다. [제곱값, 기존값]
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.predict([[50**2, 50]]))
print(lr.coef_, lr.intercept_)
=> [1573.98423528]
[ 1.01433211 -21.55792498] 116.0502107827827
앞서 훈련한 모델보다 더 높은 값을 예측한 것을 확인할 수 있다. 이제 회귀 모델 2개를 비교해서 확인해 보자(범위는 15~ 50으로)
#범위 설정
point = np.arange(15, 50)
plt.scatter(train_input, train_target)
#선형 회귀 : lr.coef_, lr.intercept_ = 39 , -709
plt.plot(point,39*point-709)
#다항 회귀 : lr.coef_, lr.intercept_ = [1.01 , -21], 116
plt.plot(point, 1.01*point**2 - 21*point + 116)
#선형 회귀 예측
plt.scatter([50], [1241], marker='v')
#다항 회귀 예측
plt.scatter([50], [1574], marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()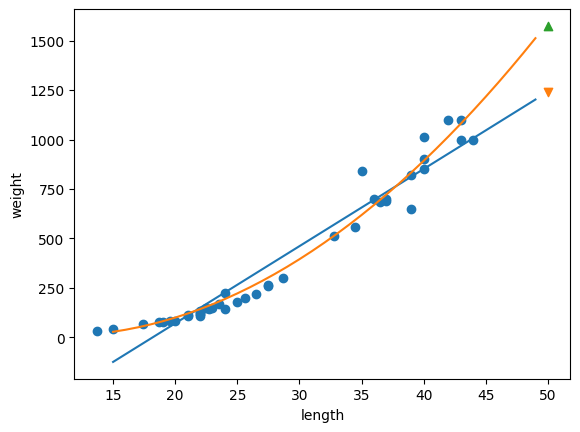
print("선형 회귀 훈련 세트 점수",lr.score(train_input, train_target))
print("선형 회귀 테스트 세트 점수",lr.score(test_input, test_target))
선형 회귀 훈련 세트 점수 0.939846333997604
선형 회귀 테스트 세트 점수 0.8247503123313558print("다항 회귀 훈련 세트 점수",lr.score(train_poly, train_target))
print("다항 회귀 테스트 세트 점수",lr.score(test_poly, test_target))
다항 회귀 훈련 세트 점수 0.9706807451768623
다항 회귀 테스트 세트 점수 0.9775935108325122선형 회귀를 사용했을 때는 두 세트 모두 점수가 낮은 과소적합이 일어나지만
다항 회귀를 사용하면 두 세트 모두 만족스러운 점수가 나오는 걸 확인할 수 있다.
'머신러닝' 카테고리의 다른 글
| 머신 러닝(with Google Colab) - 4일차(1) (0) | 2024.10.16 |
|---|---|
| 머신 러닝(with Google Colab) - 3일차(2) (4) | 2024.10.16 |
| 머신 러닝(with Google Colab) - 2일차 (0) | 2024.10.11 |
| 머신 러닝(with Google Colab) - 1일차 (0) | 2024.10.11 |
| 머신 러닝(with Google Colab) - 0일차 (6) | 2024.10.11 |