앞서 확률적 경사 하강법에 대한 설명을 끝으로 마무리 했는데 이제 실제로 사용해 보자
우선 데이터를 준비하자
import pandas as pd
fish = pd.read_csv('https://bit.ly/fish_csv')
fish_input = fish[['Weight', 'Length', 'Diagonal', 'Height', 'Width']].to_numpy()
fish_target = fish['Species'].to_numpy()
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = \
train_test_split(fish_input, fish_target, random_state=42)
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
확률적 경사 하강법을 제공하는 대표적 분류 클래스는sklearn.linear_model 패키지에 있는 SGDClassifier이다. SGDClassifier의 객체를 만들때는 2개의 중요한 매개변수가 있는데
loss 와 max_iter 이다. loss의 경우 손실함수의 종류를 지정한는데 여기서는 앞서배운
로지스틱 손실함수를 사용하므로 'log_loss'를 사용한다.
max_iter은 앞서 봤던 것이지만 여기서는 에포크의 횟수를 말한다. 에포크는 4일차에서 언급했은데 확률적 경사하강법의 과정을 반복하여 샘플을 전부 사용했을때를 1에포크라고 본다. 이제 적용해서 써보자
from sklearn.linear_model import SGDClassifier
sc = SGDClassifier(loss='log_loss',max_iter=10, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
=>0.773109243697479
0.775결과를 보면 생각보다 정확도가 낮은 것을 알수 있다. 이는 반복의 횟수가 부족해서 나온결과 일 수 있다.
앞서 확률적 경사 하강법은 점진적 학습이 가능하다고 언급했는데 그말은 지금 결과를 이어나가서 학습을 할수 있다는 것이다. partial_fit()은 fit()과 사용 방법은 같으나 기존 결과를 유지한 상태에서 1에포크를 실행한다는 의미이다. 따라서 partial_fit() 적용해 확인해 보자
sc.partial_fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
=>0.8151260504201681
0.85결과가 좋아진것을 확인할수 있다. 이를 계속 반복한다면 좋은 결과를 얻을 수 있을텐데 어떻게 해야할까
에포크의 과소/과대 적합
에포크의 학습횟수에 따라 위에서 보았드시 과소 적합이 될수 있고 너무 많이 학습하면 과대 적합이 일어날수 있다. 따라서 적절한 에포크의 값을 찾는 것 이 중요한다 이는 앞서 alpha값을 구하는 방법을 이용하면 구할수 있다.
import numpy as np
#반복횟수가 없는 형태 (1에포크)
sc = SGDClassifier(loss='log_loss', random_state=42)
train_score = []
test_score = []
classes = np.unique(train_target)
#여기서 classes 의 역할은 객채를 생성한 이후에 타겟에 대해 정해준 적이 없다 따라서 타겟을 지정해줌
#또한 반복을 할때마다 타겟에 대해 초기화를 해줄 필요도 있기 때문에
for _ in range(0,300): #굳이 반복자를 사용하지 않으면 '_'로
sc.partial_fit(train_scaled, train_target, classes=classes)
train_score.append(sc.score(train_scaled,train_target))
test_score.append(sc.score(test_scaled,test_target))여기서 classes를 따로 정해주는 이유는 지금 코드를보면 앞서 따로 fit()해주지 않아 타겟에 대한 정보가 없기 때문에 에포크를 반복하는 과정에서 타겟의 정보를 입력해줄 필요가 있기 때문이다. 이제 결과를 그림으로 확인해 보자.
#확인
import matplotlib.pyplot as plt
plt.plot(train_score)
plt.plot(test_score)
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()
sc = SGDClassifier(loss='log_loss', max_iter=100, tol=None, random_state=42)
sc.fit(train_scaled, train_target)
print('훈련 정확도',sc.score(train_scaled, train_target))
print('테스트 정확도',sc.score(test_scaled, test_target))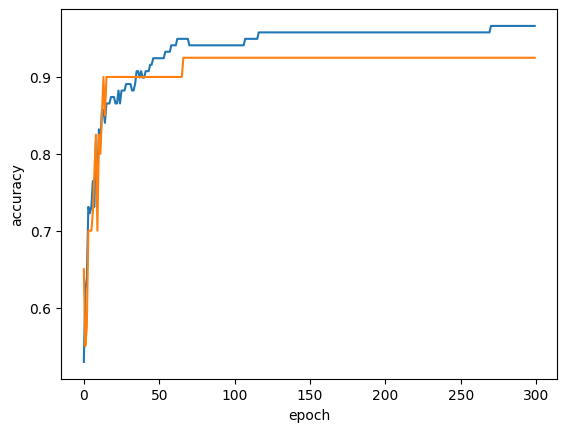
결과를 보면 100쯤에서 정확도가 좋아지고 넘어가서는 크게 변동이 없는 것을 알 수 있다. 따라서 적절한 max_iter 값은 100 근처로 설정한다면 좋은 결과를 얻을 수 있을 것이다.
훈련 정확도 0.9663865546218487
테스트 정확도 0.925
'머신러닝' 카테고리의 다른 글
| 머신 러닝(with Google Colab) - 5일차(2) (1) | 2024.10.18 |
|---|---|
| 머신 러닝(with Google Colab) - 5일차(1) (0) | 2024.10.17 |
| 머신 러닝(with Google Colab) - 4일차(1) (0) | 2024.10.16 |
| 머신 러닝(with Google Colab) - 3일차(2) (4) | 2024.10.16 |
| 머신 러닝(with Google Colab) - 3일차(1) (0) | 2024.10.14 |